Author: Rafael Vargas

The truth about Data Science…

It is just a re-branding of the Data Analytics of 10 years ago, the Data Mining of 20 years ago and the Business Intelligence of 30 years ago.

We’ve been doing machine learning (SVM, ANN, Decision trees, etc) and ETL to analyze data and produce valuable information for decision making for 20+ years now, but all of a sudden giant techs like Facebook and Google decided the title “Data Analyst” was not sexy enough, maybe because the growth of CPU power and the advent of the GPU for numerical calculations pushed the boundaries of the algorithms, e.g. deep learning, either that or they had so many PhD’s enrolled doing data analysis that they wanted to honor their job with a more coveted title.

The truth is that someone with a PhD in Statistics working at YouTube in 2006 was already employing cutting-edge stats and machine learning to find patterns in the data, but was just called a Data Analyst. 7 years later that same guy still working at YouTube doing data analysis was now called a Data Scientist. Did he care about HR changing his job name? Absolutely not. He just went on doing what he loves and ignoring fancy marketable titles like “Data Scientist”.

Oh, and also the fact that Data Science is not Science per se, since no one is following the scientific method to produce new theories that can be reproduced or falsified, nor adding to the corpus of knowledge of the field. We are merely using methods from science to aid us in our daily task, which I repeat is: producing valuable information to the Business for intelligent decision making. In this aspect a Data “Scientist” is more akin to an engineer using science rather than a physicist producing new theories.

What is the suitable mathematical model to study about the risk factor of a project?

This is a valid question for managers looking to do scenario analysis for their projects. There are several approaches to solve this, nevertheless Monte Carlo simulation is the best all-around technique for generating said scenarios.

We can use Monte Carlo methods to quantitatively assess the risk factor of a project. In this case, the main output of the simulation presents the range of possible outcomes against the probability of each value being achieved. This is usually shown as a cumulative probability plot like the following:

 

 

Here, after running n number of trials to calculate possible outcomes, the graph shows that the potential variation in total project cost is $0.7 million against a target budget value of $1.3M. The variation comes from the range of possible values between the 5th percentile – $1.1M – and the 95th percentile – $1.8M- .

The graph also shows that the probability of meeting the project cost target of $1.3 million is 25%, with a 75% of exceeding the budget. The analysis predicts an expected outcome of $1.425 million, which is an overspend of $0.125 million or ~+10%. With this data we can determine the values of total project cost that correspond to chosen confidence levels; for example there would be an 85% chance of meeting a revised budget of $1.6 million. This allows us to make risk-informed decisions trading off increased cost (+ $0.3 million, from our original $1.3 million target) against increased probability of success, i.e. from 25% to 85%.

In general, this type of analysis helps us determine how risky is the project by asking:

  • What is the potential range of variation in outcome?
    • Total potential range = $0.7 million (= 54% of project value)
    • Best case scenario = $1.1 million (–15%)
    • Worst case scenario = $1.8 million (+38%)

 

  • How likely is this project to succeed?
    • Probability of meeting $1.3 million target = 25%
    • Expected value = $1.425 million (+10%)

A mathematical model for the change in the duration of daylight as we progress from solstice to equinox

This is an interesting problem to try and figure out. We will propose a trigonometric approach: since the seasons of the year are cyclic events, we can model daylight oscillations after a sine or cosine function.

Caveat: this model is not universal and depends on the actual sunrise and sunset times for a given place. Nevertheless, this actually makes sense, since the distribution of daylight across the globe is not uniform, but a function of the latitude and current season of said location.

First, let’s pick a place for our analysis, let’s say Seattle, WA in the US. Then let’s define the amplitude and period for the function based on the selected location.

Finding the amplitude

Knowing that the solstices are the high and low points of daylight, we look for the daylength of these two points of the year. We will use data from http://www.timeanddate.com:

Then,

Daylength 21 Jun = DL_A = 16 hrs

Daylength 21 Dec = DL_B = 8.42 hrs

Amplitude = \frac{DL_A - DL_B}{2} = \frac{16 - 8.42}{2} = 3.79 hrs

The average daylight throughout the year is given by average(DL_A, DL_B) which is 12.21 hrs. This way we have 12.21 \pm 3.79 hrs.

Finding the period

The period of the sine/cosine is 2\pi, but since we need to express this in days we divide 2\pi by 365t to actually have the proportion of the period covered by a time t within one cycle of the curve (effectively a year).

Daylight equation

Defining the highest daylight point (June 21) as t=0, we can now have an equation that models the change from peak to minimum daylight for a time t and a given location, in this case Seattle.

f(t) = 3.79/cos (2\pi/365t) +12.21

Is mathematics a language?

This is a question that people often ask and find themselves answering that yes, mathematics is indeed a language, because it uses particular symbols to convey information and carries meaning in itself. From the definition of language we have:

A language is a system that consists of the development, acquisition, maintenance and use of complex systems of communication, particularly the human ability to do so; and a language is any specific example of such a system.

source: Wikipedia

But, is this really fully compatible with the definition of mathematics? Is language the only thing mathematics is about, or does it have a deeper reality? From the definition of the same source:

Mathematics includes the study of such topics as quantity, structure, space, and change. Mathematicians seek and use patterns to formulate new conjectures; they resolve the truth or falsity of conjectures by mathematical proof.

From this we see that mathematics is not a language per se. Even though it uses rigorous formalisms and logic to formulate its postulates, those are only the methods of conveying information more than its underlying ontological reality: mathematics is the abstract study of patterns.

In a sense, it is a bit like music. Some people say music is a language, but it is not. Music is a reality deeper than the symbols it uses to try to frame and categorize its own concepts.

A language is an end in itself because it has a grammar and rules with the only purpose of communicating ideas, but it doesn’t carry any underlying reality. Music and mathematics use a type of language, but are not languages themselves.

Orbital Resonance and Just Intonation

In celestial mechanics, an orbital resonance occurs when orbiting bodies exert a regular, periodic gravitational influence on each other, usually because their orbital periods are related by a ratio of small integers

 

Jupiter and three of its Galilean moons

 

This concept is analogous to the definition of Just Intonation, in which the frequencies of notes are related by ratios of small whole numbers. So this got me thinking, what chord intervals would these orbits produce if we could hear them?

This tables shows the ratios of the intervals between two notes for two octaves:

C D E F G A B C’ D’ E’ F’ G’ A’ B’ C”
C 1 9/8 5/4 4/3 3/2 5/3 15/8 2 9/4 5/2 4/3 3 10/3 15/4 4

If we extrapolate these to the orbits of the picture above, we have that Jupiter and IO have an unison interval, Europa would produce an octave and Ganymede would be two octaves higher than the fundamental frequency or, in this case, orbit of Jupiter.

Also Neptune and Pluto have a 3:2 orbital resonance, which gives us would gives us a G frequency sound. Other resonances of interest are:

  • In the asteroid belt within 3.5 AU from the Sun, the Kirkwood gaps, most notably at the 4:1, 3:1, 5:2, and 2:1 resonances, or a 15ma, a fifth over the octave, a tenth and an octave above the fundamental frequency respectively.

 

  • Asteroids of the Alinda family are in or close to the 3:1 resonance, which yields a G one octave above the fundamental

 

Why can’t some people stay focused unless they are listening to music?

Let me introduce you to this guy

Yes. That’s the great John Von Neumann [^1], one of the brightest minds of all time. He made huge contributions to human knowledge, from Mathematics to Physics to Computer Science to Economics to a plethora of other topics.

Von Neumann was an interesting character both, personally and scientifically. While working at the Institute of Advanced Study in Princeton he used to play loud classical music in order to concentrate and keep focus, much to the annoyance of his colleagues which included Einstein and Gödel. Also, he once got mad at his wife for preparing a quiet study for him to work in, preferring to work in the living room with the TV on high volume.

But why are there people who only seem to concentrate in a loud or chaotic ambient? Regarding the wiring of the brain this might have to do with our Attention Mechanisms [^2].

Human beings have two layers of attention, one conscious and one unconscious. The conscious one enables us to direct our focus towards things we know we want to concentrate on. The unconscious one shifts our attention towards anything our senses pick up that might be significant in the surroundings.

The unconscious one is simpler, more fundamental, and linked to emotional processing rather than higher reasoning. It also operates faster and it’s constantly on. This means that when you try to consciously concentrate on a task, part of your brain is still picking up signals in the background environment that interfere with your focus. If said task is boring or unattractive to you then this interference is even stronger and you won’t need much external distraction to lose concentration. You then enter a vicious cycle of trying to force your conscious attention system to stay focused, generating fatigue and raising the probability of getting distracted even more.

This is where listening to music plays a significant role, by feeding your unconscious attention mechanism with something constant, consistent and coherent to focus in. The more you like the music, the more you will focus – obviously if you don’t like the music it will only add up to the dullness of the active attention task…but who listens to music one doesn’t like anyway?

Everyone is different and there are people that can better control their unconscious attention mechanism, or rather they don’t have it as on as others might. This doesn’t mean you have a problem or that one type is better than the other, it’s just who you are. Make the best of it.

References:

[1] John von Neumann

[2] Does music really help you concentrate?

What mathematical models affect our daily lives?

Mathematics, like grammatical language, is part of our daily lives and it’s present in virtually everything we do, even if we are not consciously aware of it. Below, I list some of the mathematical models that are pretty connected to our everyday lives.

Demand of goods and services

Maybe the most obvious and well-known. It is given by:

\displaystyle{Q_x = f(P_x,\textbf{C}) ; \hspace{3mm} and \hspace{3mm}\frac{\partial f}{\partial P_x} < 0},

where,

x : A given Good or Product

Q_x : Quantity of said Good

P_x : Price of Good

C: Ceteris Paribus condition (i.e. keeping constant every other factor that may impact demand)

f : Demand Function

\displaystyle{\frac{\partial f}{\partial P_x}} : first partial derivative of the Demanded Quantity with respect to Price (rate of change of the quantity for every variation in the price).

This rate of change shows to be $latex< 0$, which indicates the well-known statement as the price increases, quantity demanded decreases and vice versa. Likewise, when there is an abundance of a given good, price tends to decrease due to its availability and “non-rarity”; but if the good is scarce then the price will go up because buyers will be willing to pay higher amounts of money to get it.

Queuing and Traffic Models

Two examples here:

  • The queueing models used by customer care service in banking, telecom and, in general, any system requiring to estimate the amount of individuals that will be in queue waiting to be served by n representatives (servers) in a given period of time. These events follow a Poisson probability distribution and can be modeled using the so called Poisson processes. Poisson distribution is given by:

\displaystyle{P\left({n} \right) = \frac{{e^{ - \lambda } \lambda ^n }}{{n!}}}

where,

n : Number of observed events

\lambda : Average numbers of events per time interval

e : Exponential Constant

n! : n factorial [n(n-1)(n-2)…(2)(1)]

  • The network traffic models used by telephone service providers to calculate network congestion and guarantee QoS (quality of service). Traffic is usually modeled following an Erlang distribution, whose probability density function is given by the following expression:

\displaystyle{f(x;k,\lambda )={\lambda ^{k}x^{{k-1}}e^{{-\lambda x}} \over (k-1)!}\quad {\mbox{for }}x,\lambda \geq 0}

Risk Models

They are used to estimate outcomes in several scenarios, among them the risk of granting x amount of money in loan to a given person. Also, they are used to model survival: the probability that a specific customer continues with the company after any given specified time, or that a patient survives after a future time T. Survival is modeled by:

\displaystyle{S(t)=P(\{T>t\})=\int _{t}^{\infty }f(u)\,du}

Which is the same as to say that survival is the complementary function of the cumulative distribution function, or =1-F(t), where F(t) is the cumulative distribution function

Meteorological Models

We all have seen (and experienced) weather forecasts and atmospheric phenomena follow-up models. These models, named CLIPER (climate and persistence), use Multiple Linear Regression methods to predict climate behavior.

Multiple linear regression equation is given by:

{\displaystyle Y_{i}=\beta _{0}+\sum \beta _{p}X_{pi}+\varepsilon _{i}}

where,

Y_i : forecasted variable

\beta_0 : Y axis intercept; or the average constant value of a forecasted variable Y when all X values given to estimate it are equal to 0

\beta_p : Regression slope; i.e., how much does the Y forecast change for every change in each X component used to predict it

X_{pi} : Components impacting the forecasted variable

\varepsilon_i : Estimation error

All these examples, and the ones detailed in the other answers, show that mathematical models are indeed part of our daily lives. Some may look more complex than others, but the intuition is simple and easy to follow. The important part is not the calculations per se, but the awareness that we can put mathematics to use in a lot of everyday situations and, in this way, help to demystify a bit all things pertinent to this discipline.

A tale about product differentiation

Imagine your are looking for a job. Today you have an interview for a position in Marketing in Company T. You dressed up nice, full suit, tie on, nice black shoes. The whole corporate combo.

You approach Company T’s HQ and go right to the Reception Desk, asking for guidance about the interview. The host directs you to the 7th floor where the office of the Senior Manager is located. While going up in the elevator, you recap the speech you are going to say and imagine tricky questions and scenarios that may be thrown at you, to prepare answers in advance.

You arrive at the 7th floor and the first thing you notice is 8 more guys about your age, dressed almost exactly like you. -“It’s alright” – you say to yourself, feeling a little awkward – “No one is gonna hire or reject anyone just based on looks and/or similar appearance”-. You sit down and engage in some small talk with the other candidates only to quickly find out they are also pretty smart and have a coveted degree from a top university, just like you.

By this point you are beginning to feel nervous. It never occurred to you that the competition would be so strong. A door opening interrupts your thoughts. -“Thank you. We will be contacting you. Next, please”- The next guy in the line stands up, adjusts his tie, combs his hair and goes on to the interview.

The same process repeats until it’s finally your turn. You stand up, adjust your tie, comb your hair and enter the office for the interview. As you enter, the Senior Manager prompts you to sit down. He doesn’t say anything for a moment, he is just sitting there examining you and your composure. You break the silence by saying -“Sir, let me start by saying it’s an honor to be offered a job interview in this great Company”- to which he replies – “I’ll tell you something, since you are the last one today and I’m really tired: Can you tell me in 5 sentences why should i hire you and not one of the other 9? They all felt privileged to be offered a position in this Company, they are more or less your age and they all have either your same degree of similar enough for the job. How’d you make it easy for me to know you are the perfect person for this position?

Here you pause for a moment and go inside yourself looking for that something unique and special that only you have and can deliver to others. Arising from your inner depths, a smile on your face begins to tell the answer:

– “I’m not the perfect person for this position, I’m the best person for this position. I know pretty well how to manage the trade off between launching a good product in time vs launching a perfect product and lose market momentum. I know how to get my ideas across and convince people to take my route, but also accept when ‘it is what it is’. I’m highly resilient and know how to deal with pressure and cope with disappointment, not only mine but my team’s. Finally, I will work my butt off and show results before asking for any extraordinary bonus, since there’s absolutely no one more critical of my work than myself, so I’ll always be one step ahead of you in that aspect”.

Impressed, the Senior Manager tells you – “HR will be contacting you later this week”- he shakes your hand and dismisses you. Certainly a few days later you receive a call from Company T’s HR Dpt. You’ve been accepted to the position and begin to work next week. You are so happy that the next Monday arrives so fast you didn’t even noticed. You are on your first day of work, accommodating your new home outside your home. It’s almost lunch time and you ask some of your coworkers where to eat. He tells you of a nice place across the street and you go to give it a try. There you find one of the former candidates who recognizes you and sees your new ID Card from Company T – “Product Dev Analyst. Cool dude, congratulations on getting the job! How did the interview go?”- you proceed to recount the interview details when suddenly he stops you – “Wait, What!? He also told you that he was tired and that all other guys before you said the same thing as you did? Dude, you reeaally did say something different that caught his eye then. The first guy interviewed that day is one of my best friends from college. We agreed to accept and congratulate whichever would get the job. He confessed to me that the Senior Manager told him all the other candidates said exactly the same speech as him and that he was tired from interviews from the day before! He said the same thing to me…and apparently to everybody!”

This is when you fully started appreciating the value of differentiation in a saturated market, full of similar options. In order to win, you need to have something to distinguish yourself from the pack, be sexy. Smiling again at your realization, you go back to work with a sandwich in your right hand and with this thought in your head: “I gotta apply this exact thing to my products and services at work”.

What is a Mathematical Model?

P5-Mathematical-05-BB-1406-04

 

A Mathematical Model is an abstraction of a real-life scenario, system or event that uses mathematical language to describe and predict the behavior, dynamics and evolution of said scenario, system or event.

Mathematical Modelling is thus the step-by-step process of performing this abstraction from real scenarios to equations and formulas we can use to infer their characteristics. This is better visualized by the following diagram:

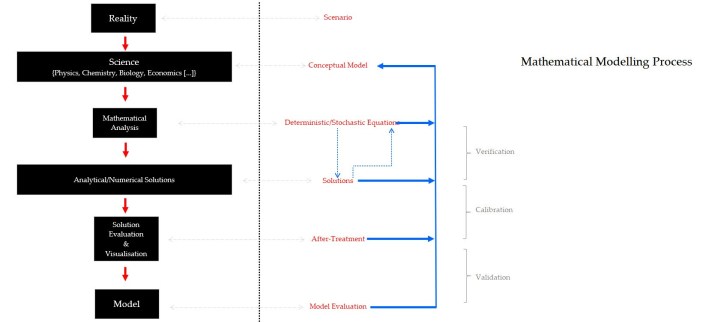
mathmodelling1.jpg

Reality is studied by Science and its different branches, known as disciplines. These disciplines conceptualize Reality, each in their own way within their area of study. For example, Physics and Chemistry study nature’s structure, Biology deals with living beings and Economics tries to explain production and consumption of goods and services. These conceptualizations are then formulated as mathematical equations, either deterministic (fixed) or stochastic (partially random), depending on the nature of the scenario or system.

Once the equations are formulated, they are solved to find solutions depicting the behavior, dynamics and evolution of the their real-life counterparts. Upon evaluation, these solutions may not be accurate when contrasted with observed experimental data and might need calibration and adjustment. If no progress is achieved, the process goes back one step to find a better equation defining the system.

Once the equations and solutions are verified and calibrated, the model is validated when it accurately describes Reality and its results can be shown to be reproducible and repeatable across the Scientific community.

Mathematical Models need to be reviewed from time to time to confirm if they are still relevant. As the disciplines and systems evolve, they may be updated or even replaced with new ones better depicting Reality. This is why mathematical models are at the core of the Scientific Method principle of falsifiability, providing a direct way to evaluate solutions, update descriptions and create new theories.

but…

Why do we use abstract mathematical models when we could develop physical models?

Abstractions are good because they generalize patterns, behaviors, outcomes and realities without having to physically construct a model. Even if you develop a physical model, which is very good to actually see how a system outcome would look, it wouldn’t say much about the inner rules governing that system.

In general, Nature already has a physical model constructed for us called Reality and we just want to know how to predict the behavior and outcome of the systems that form that Reality.

Let’s take our Solar System for example. We could build a replica one trillionth its actual size and sure enough you will have accurately depicted the size of the planets and the Sun, the length between them, their moons and their orbits. If we throw in an incandescent bulb with the appropriate power and placing it within the Sun, we will also have shown irradiance and even the temperature of the Solar System space, but the keyword here is shown. We could continue to add as many features as humanly possible to the model, to make it as accurate as the real thing, but the fact remains we are are only describing a steady state: we are not actually gaining any insight about the dynamics of the system, we are not exploring how variables interact with each other and how internal conditions can affect its outcome. Furthermore, we cannot make predictions at all, because we don’t have a general abstraction that receives inputs, process them and then gives us back the output of the system variables.

Physical models need to be used in tandem with mathematical models if we are to derive some concrete insight from them. Now, let’s imagine we have an aeronautical engineer and we need to simulate a plane’s behavior at a given altitude, subjected to X pressure and Y air velocity, among other things. Our engineer proceeds to build a physical model of the plane and a wind tunnel to test air dynamics and how it interacts with your scaled-down model. She puts the plane model inside the tunnel, turn on the wind simulation (fan) and then with the aid of a mathematical model (Bernoulli’s principle, Reynolds number and Mach number in this case) she makes the necessary adjustments to guarantee the optimal production of a real sized plane.

Image Source: Wikipedia

Without the actual mathematical model, it would not be possible to make efficient adjustments. Imagine if we always had to build a physical model for everything we wanted to describe, or if we had to build several models for every scenario we wanted to extract information from. Besides the time, effort and financial cost, the models wouldn’t be able to tell us much, apart from a good visual representation. Even prototypes are built after doing the math and not the other way around, to optimize the above mentioned factors.

The good news are that recent advance in computational simulation is rendering the need of using a physical model unnecessary in many areas, while in others they are continued to be used together with the computer simulated/mathematical models; such as in the case of our wind tunnel example in the field of Aerodynamics.

Musimathician | Ready. Set. Go!

The worst foe lies within the self. — Aya Brea @Parasite Eve  Christmas 1997

Hello dear reader,

Let us explore together the interweaving of the musimathical cosmos, deep into the harmonies of the universe and the resonance of orbiting galaxies within major 7th chords.

In this blog we will discuss about music, mathematical modeling and statistics, business economics and marketing, literature, astronomy and the conjunction of all the above into one and one into all.

All things must have a beginning. Let us declare ours right here and not worry about the end.

Enjoy.

post